Evolutionary genomics inference methods
We develop methods to infer population genetics parameters from genetic/genomic data.
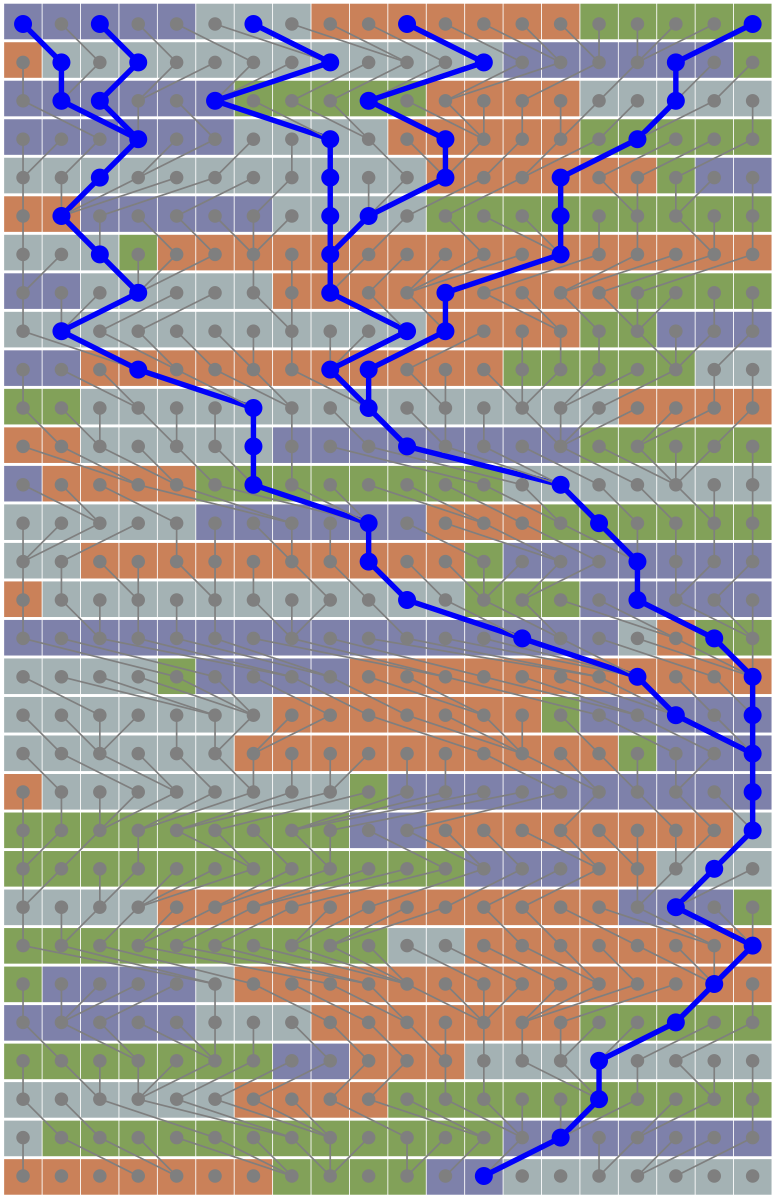
The fractional coalescent
Abstract from our paper: An approach to the coalescent, the fractional coalescent (f-coalescent), is introduced. The derivation is based on the discrete- time Cannings population model in which the variance of the number of offspring depends on the parameter α. This additional parameter α affects the variability of the patterns of the waiting times; values of α<1 lead to an increase of short time intervals, but occasionally allow for very long time intervals. When α=1, the f-coalescent and the Kingman’s n-coalescent are equivalent. The distribution of the time to the most recent common ancestor and the probability that n genes descend from m ancestral genes in a time interval of length T for the f-coalescent are derived. The f-coalescent has been implemented in the population genetic model inference software MIGRATE. Simulation studies suggest that it is possible to accurately estimate α values from data that were generated with known α values and that the f-coalescent can detect potential environmental heterogeneity within a pop- ulation. Bayes factor comparisons of simulated data with α<1 and real data (H1N1 influenza and malaria parasites) showed an improved model fit of the f-coalescent over the n-coalescent. The development of the f-coalescent and its inclusion into the inference program MIGRATE facilitates testing for deviations from the n-coalescent.
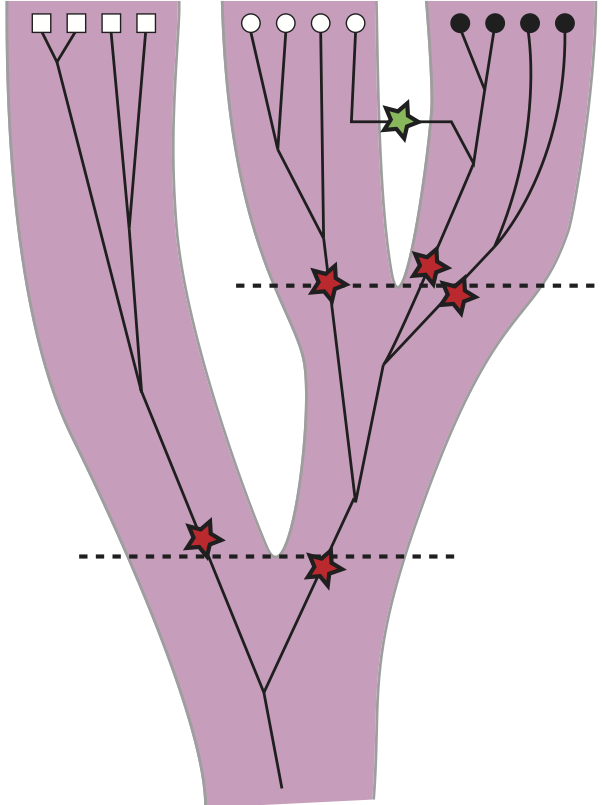
Inference of population splitting times
Most recently we have worked on estimation of population splitting times. This method is an alternative to other programs. We strive to develop methods that can be run on large computer clusters in parallel and thus harness the power of many sequence loci. We believe that methods depending on site frequency spectra of single nucleotide polymorphisms are potentially biased and eventually once our methods are faster then they are now we may be able to do a straight comparison.
Standard divergence time estimates in population genetics are treating the divergence time as a parameter that changes during the makrov Chain Monte Carlo run according to some prior distribution. We treat the splitting time as a random variable; it is the mean and standard deviation of a truncated Normal distribution (we could use other distributions as well), we use MCMC and prior distributions to change this mean and the standard deviations. This approach allows to treat splitting events similar to migration events on the genealogies. If the signal in the data is very clearly favoring a consistent split among populations then the posterior distribution of standard deviation should peak at zero, whereas if the (biological) splitting process is a more drawn out process, then the standard deviation will be large; for example incomplete separation of the populations for some time due to immigration.
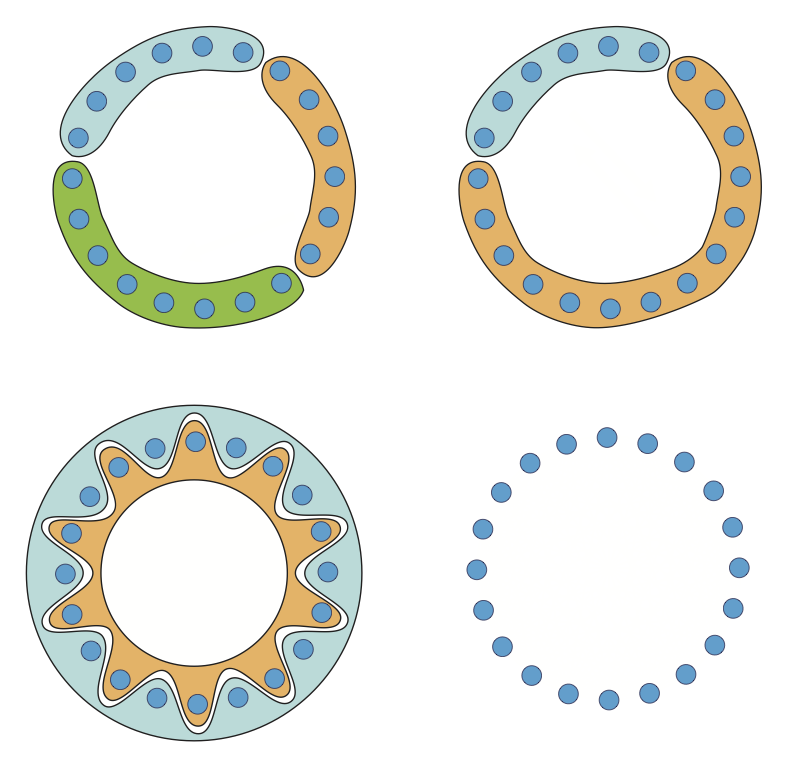
Model selection
Michal Palczewski and I have written two papers that discuss the comparison of population genetic models in a Bayesian context. We calculate marginal likelihoods that allow comparing nested or unnested models, we used thermodynamic integration to approximate the marginal likelihoods, (1) our paper in Genetics 2010 and the tutorial on our main software MIGRATE website seems have inspire many researchers to compare different hypotheses not only qualitatively in the discussion but also quantitatively. (2) In a book chapter we have detailed our approach. In particular, we highlight how we combine individually analyzed loci for a combined marginal likelihood.
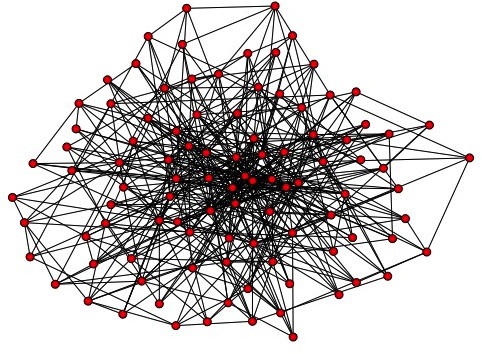
Hidden Markov models to detect Social network structure
Author: Haleh Ashki and Peter Beerli. a preview of the abstract of our (soon to be submitted) paper: [REVISION MARCH 24 2017] The social contact network among host individuals and the genealogy of the pathogen are main components influencing disease transmission. Current gene sequencing technologies have opened a new gateway in epidemiology research because they allow tracking the mutational changes of the disease agent during the course of an epidemic. Several method exist to track past transmission patterns, but these methods have not been used in a prospective manner to demonstrate how the underlying population interactions relate to viral evolution and transmission. Here, we present an approach using a Hidden Markov Model to jointly reconstruct the phylogenetic history of a pathogen and the dynamic contact network of its host. We combine epidemiological modeling and genomic information to reconstruct a dynamic contact network that may help to prospectively intervene in a population using detailed sequence and network data.
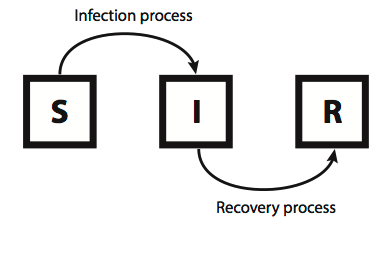
Dynamics of an epidemic and intervention method on weighted dynamic networks
Author: Haleh Ashki and Peter Beerli. Contact networks among individuals have a great impact on the propagation of epidemic diseases. The structure of this contact network is dynamic. We combined the epidemiological SIR model with a dynamic network that is represented as a weighted adjacency matrix. Our approach solves a single equation for each individual at every time step. The effect on disease dynamics is shown using simulated static and dynamic networks and with a real dynamic contact network recorded by Salathe 2010.. Simulated intervention on important nodes, identified by their Page rank, in these dynamic networks can be used to explore effective measures to reduce the epidemic.